window._wpemojiSettings = {"baseUrl":"https:\/\/s.w.org\/images\/core\/emoji\/15.0.3\/72x72\/","ext":".png","svgUrl":"https:\/\/s.w.org\/images\/core\/emoji\/15.0.3\/svg\/","svgExt":".svg","source":{"concatemoji":"https:\/\/www.uniquenewsonline.com\/wp-includes\/js\/wp-emoji-release.min.js?ver=6.5.3"}};
/*! This file is auto-generated */
!function(i,n){var o,s,e;function c(e){try{var t={supportTests:e,timestamp:(new Date).valueOf()};sessionStorage.setItem(o,JSON.stringify(t))}catch(e){}}function p(e,t,n){e.clearRect(0,0,e.canvas.width,e.canvas.height),e.fillText(t,0,0);var t=new Uint32Array(e.getImageData(0,0,e.canvas.width,e.canvas.height).data),r=(e.clearRect(0,0,e.canvas.width,e.canvas.height),e.fillText(n,0,0),new Uint32Array(e.getImageData(0,0,e.canvas.width,e.canvas.height).data));return t.every(function(e,t){return e===r[t]})}function u(e,t,n){switch(t){case"flag":return n(e,"\ud83c\udff3\ufe0f\u200d\u26a7\ufe0f","\ud83c\udff3\ufe0f\u200b\u26a7\ufe0f")?!1:!n(e,"\ud83c\uddfa\ud83c\uddf3","\ud83c\uddfa\u200b\ud83c\uddf3")&&!n(e,"\ud83c\udff4\udb40\udc67\udb40\udc62\udb40\udc65\udb40\udc6e\udb40\udc67\udb40\udc7f","\ud83c\udff4\u200b\udb40\udc67\u200b\udb40\udc62\u200b\udb40\udc65\u200b\udb40\udc6e\u200b\udb40\udc67\u200b\udb40\udc7f");case"emoji":return!n(e,"\ud83d\udc26\u200d\u2b1b","\ud83d\udc26\u200b\u2b1b")}return!1}function f(e,t,n){var r="undefined"!=typeof WorkerGlobalScope&&self instanceof WorkerGlobalScope?new OffscreenCanvas(300,150):i.createElement("canvas"),a=r.getContext("2d",{willReadFrequently:!0}),o=(a.textBaseline="top",a.font="600 32px Arial",{});return e.forEach(function(e){o[e]=t(a,e,n)}),o}function t(e){var t=i.createElement("script");t.src=e,t.defer=!0,i.head.appendChild(t)}"undefined"!=typeof Promise&&(o="wpEmojiSettingsSupports",s=["flag","emoji"],n.supports={everything:!0,everythingExceptFlag:!0},e=new Promise(function(e){i.addEventListener("DOMContentLoaded",e,{once:!0})}),new Promise(function(t){var n=function(){try{var e=JSON.parse(sessionStorage.getItem(o));if("object"==typeof e&&"number"==typeof e.timestamp&&(new Date).valueOf()<e.timestamp+604800&&"object"==typeof e.supportTests)return e.supportTests}catch(e){}return null}();if(!n){if("undefined"!=typeof Worker&&"undefined"!=typeof OffscreenCanvas&&"undefined"!=typeof URL&&URL.createObjectURL&&"undefined"!=typeof Blob)try{var e="postMessage("+f.toString()+"("+[JSON.stringify(s),u.toString(),p.toString()].join(",")+"));",r=new Blob([e],{type:"text/javascript"}),a=new Worker(URL.createObjectURL(r),{name:"wpTestEmojiSupports"});return void(a.onmessage=function(e){c(n=e.data),a.terminate(),t(n)})}catch(e){}c(n=f(s,u,p))}t(n)}).then(function(e){for(var t in e)n.supports[t]=e[t],n.supports.everything=n.supports.everything&&n.supports[t],"flag"!==t&&(n.supports.everythingExceptFlag=n.supports.everythingExceptFlag&&n.supports[t]);n.supports.everythingExceptFlag=n.supports.everythingExceptFlag&&!n.supports.flag,n.DOMReady=!1,n.readyCallback=function(){n.DOMReady=!0}}).then(function(){return e}).then(function(){var e;n.supports.everything||(n.readyCallback(),(e=n.source||{}).concatemoji?t(e.concatemoji):e.wpemoji&&e.twemoji&&(t(e.twemoji),t(e.wpemoji)))}))}((window,document),window._wpemojiSettings);
https://www.uniquenewsonline.com/wp-includes/js/jquery/jquery.min.js
https://www.uniquenewsonline.com/wp-includes/js/jquery/jquery-migrate.min.js
var pbLocalizeObj = {"ajax":"https:\/\/www.uniquenewsonline.com\/wp-admin\/admin-ajax.php","seconds":"seconds","thisWillClose":"This will close in","icons":{"close_icon":"<svg class=\"ays_pb_material_close_icon\" xmlns=\"https:\/\/www.w3.org\/2000\/svg\" height=\"36px\" viewBox=\"0 0 24 24\" width=\"36px\" fill=\"#000000\" alt=\"Pop-up Close\"><path d=\"M0 0h24v24H0z\" fill=\"none\"\/><path d=\"M19 6.41L17.59 5 12 10.59 6.41 5 5 6.41 10.59 12 5 17.59 6.41 19 12 13.41 17.59 19 19 17.59 13.41 12z\"\/><\/svg>","close_circle_icon":"<svg class=\"ays_pb_material_close_circle_icon\" xmlns=\"https:\/\/www.w3.org\/2000\/svg\" height=\"24\" viewBox=\"0 0 24 24\" width=\"36\" alt=\"Pop-up Close\"><path d=\"M0 0h24v24H0z\" fill=\"none\"\/><path d=\"M12 2C6.47 2 2 6.47 2 12s4.47 10 10 10 10-4.47 10-10S17.53 2 12 2zm5 13.59L15.59 17 12 13.41 8.41 17 7 15.59 10.59 12 7 8.41 8.41 7 12 10.59 15.59 7 17 8.41 13.41 12 17 15.59z\"\/><\/svg>","volume_up_icon":"<svg class=\"ays_pb_fa_volume\" xmlns=\"https:\/\/www.w3.org\/2000\/svg\" height=\"24\" viewBox=\"0 0 24 24\" width=\"36\"><path d=\"M0 0h24v24H0z\" fill=\"none\"\/><path d=\"M3 9v6h4l5 5V4L7 9H3zm13.5 3c0-1.77-1.02-3.29-2.5-4.03v8.05c1.48-.73 2.5-2.25 2.5-4.02zM14 3.23v2.06c2.89.86 5 3.54 5 6.71s-2.11 5.85-5 6.71v2.06c4.01-.91 7-4.49 7-8.77s-2.99-7.86-7-8.77z\"\/><\/svg>","volume_mute_icon":"<svg xmlns=\"https:\/\/www.w3.org\/2000\/svg\" height=\"24\" viewBox=\"0 0 24 24\" width=\"24\"><path d=\"M0 0h24v24H0z\" fill=\"none\"\/><path d=\"M7 9v6h4l5 5V4l-5 5H7z\"\/><\/svg>"}};
https://www.uniquenewsonline.com/wp-content/plugins/ays-popup-box/public/js/ays-pb-public.js
var breeze_prefetch = {"local_url":"https:\/\/www.uniquenewsonline.com","ignore_remote_prefetch":"1","ignore_list":["\/wp-admin\/"]};
https://www.uniquenewsonline.com/wp-content/plugins/breeze/assets/js/js-front-end/breeze-prefetch-links.min.js
Unique News Online
Standard Deviation – The Best Measure of Dispersion
Standard Deviation – The Best Measure of Dispersion Published
2 years ago on
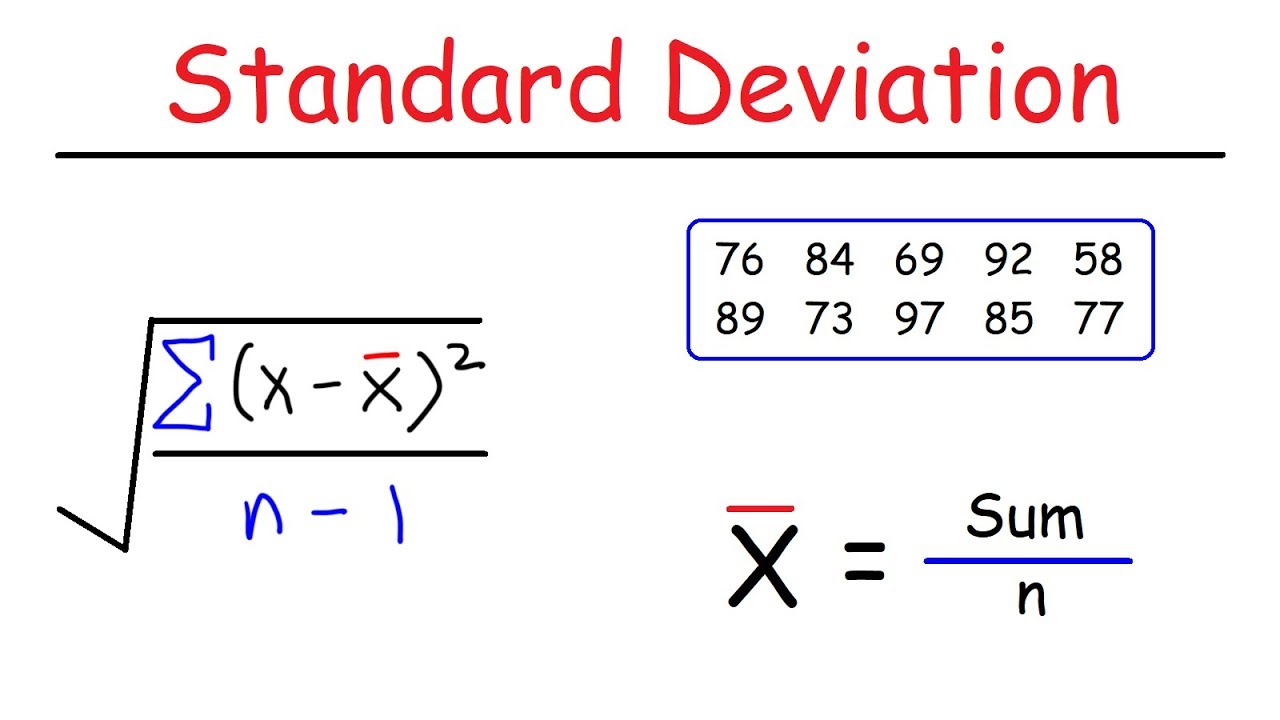
December 24, 2021 You might have learned about the standard deviation formula in your maths classes. Did you find it confusing? Do not worry. We will see in detail what a standard deviation formula is and the different properties related to it. A standard deviation is an absolute form of dispersion that is widely used to measure the scatteredness of any given distribution. It is considered the best measure of dispersion as it does not possess the demerits of other forms of absolute forms of dispersion like range and mean deviation.
The standard deviation for a given set of observations is defined as the root mean square deviation when the deviations are taken from the arithmetic mean of the observations. If a variable x assumes n values x1 , x2 , x3 , …., xn then its standard deviation (s) is given by
S = √ (∑ (x – x̄) (x – x̄) / n)
This formula is for simple or discrete frequency distribution. For a grouped frequency distribution, the standard deviation is given by
S = √ (∑ f (x – x̄) (x – x̄) / N)
Sometimes the square of standard deviation, known as variance, is regarded as a measure of dispersion. Thus, variance = square of the standard deviation.
We can also calculate a relative measure of dispersion known as the coefficient of variation using the standard deviation. The coefficient of variation is defined as the ratio of standard deviation to the corresponding arithmetic mean, expressed as a percentage.
Coefficient of Variation ( CV ) = ( Standard deviation / Arithmetic mean ) / 100
Also Read: Albert Einstein Nobel Lecture
Let us see an example and understand the calculation of standard deviation using the formula given above. We need to find the arithmetic mean, variance, and standard deviation for the following numbers: 5, 8, 9, 2, 6.
Solution: We know,
Arithmetic Mean = Sum of given observations / Total number of observations.
Thus, Arithmetic Mean = ( 5 + 8 + 9 + 2 + 6 ) / 5 = 6
Now, ∑x.x = 25 + 64 + 81 + 4 + 36 = 210
Variance = 210/5 – 6.6 = 42 – 36 = 6
We have learned before that variance is the square of standard deviation.
Thus, standard deviation = √6 = 2.45
1. If all the observations assumed by a variable are equal or constant, then the standard deviation is zero. This means that if all the values taken by a variable x is k, then the standard deviation = 0. This property is also applicable to range as well as the mean deviation.
2. Standard deviation is not affected due to a change of origin but is affected in the same ratio due to a change of scale which means that if there are two variables x and y related as y = a + b. x for any two constants a and b, then the standard deviation of y is given by
The standard deviation of y = | b | Standard deviation of x.
3. For any two numbers a and b, standard deviation is given by | a – b | / 2.
Cuemath is one of the best online tutoring platforms that teach maths as life skills and not just as school subjects. It provides one-to-one live sessions with the best tutors that ensure that all your doubts are cleared and you gain conceptual clarity in complex topics. Visit the Cuemath website and book a free session with them and learn from the experts that care and have a passion for teaching. Let us now proceed to understand what a standard deviation is.
Heana Sharma: A rising talent, Heana boasts 2 years of versatile content writing experience across multiple niches. Her adaptable skills result in engaging and informative content that resonates with a wide spectrum of readers.
Report: NEET SS 2024 May Not Be Conducted This Year Due to the Admission Delay of the 2021 Batch Published
7 days ago on
May 1, 2024 An RTI or Right to Information request was submitted by Dr Vivek Pandey, an activist, regarding the advancement of the NEET PG 2024 examination.
The NMC, National Medical Commission has responded to the request regarding the National Eligibility cum Entrance Test Postgraduate (NEET PG) 2024 test.
The same reply by NMC also revealed the status of the NEET SS (Super Specialty) examination for the current academic year. It is anticipated that NEET SS 2023 might not take place this year.
As per the RTI, the 2021 academic year admission procedure for DNB and MD/MS courses took place from January to May 2022. Thus, the chances of NEET SS 2024 being conducted this year are low.
RTI further added that the exact date of the examination in 2023 or 2025 will be decided in the future, reports India.com .
About The Minutes of the Meeting of NMC Dr Vivek Pandey shared the Minutes of Meeting of NMC. It quoted,
“Regarding NEET SS 2024, it was decided that as admissions for academic year 2021 for MD, MS and DNB courses were held only in January to May 2022, therefore, NEET SS 2024 may not be conducted in the current year. However, the exact date of conducting NEET SS 2024 in the year 2025 will be decided later.”
The meeting took place on February 21. It was chaired by the President of the Post-Graduate Medical Education Board, Dr Vijay Oza.
As per Shiksha , other participants in the meeting included the Deputy Secretary, PGMEB, NMC: Sh Aujender Singh; Joint Director, NBEMS: Dr Vinay Gupta; Dr Rakesh Sharma OSD, NBEMS; Dr B Srinivas, DDG (ME), MCC and Secretary, NMC; Prof M Bajpai, Hony Executive Director of NBEMS.
The panel finalized the date of the NEET PG 2024 examination. It has been finalized to be conducted on June 23, 2024.
The panel discussed the pattern of examination of the upcoming NEET SS.
Until now, the entire schedule of the NEET SS 2024 examination has not been revealed yet. However, it will be announced, once decided.
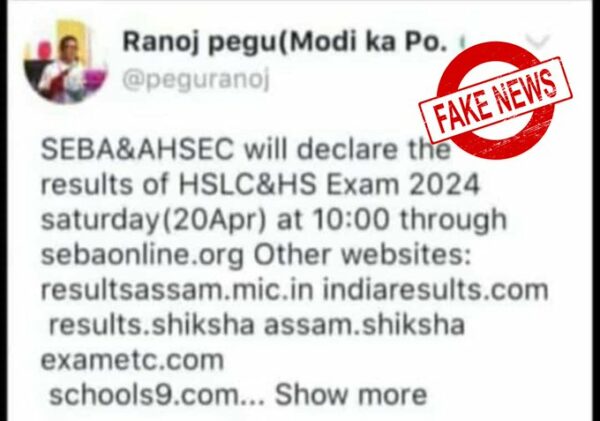
Also Read: Assam Education Minister Ranoj Pegu Exposes Fake Twitter Account Spreading Rumors on HSLC Exam Results, Shares Screen Shot On Social Media
Assam Education Minister Ranoj Pegu Exposes Fake Twitter Account Spreading Rumors on HSLC Exam Results, Shares Screen Shot On Social Media Published
3 weeks ago on
April 20, 2024 It was another case of fake news in which a rumor spread that the results of Assam Higher Secondary exams had been released. The fake news spread quickly, requiring the intervention of Assam’s Education Minister, Ranoj Pegu, who exposed the details of a fake Twitter account spreading rumors about exam results.
On Friday, Assam’s Education Minister, Ranoj Pegu, took to social media to debunk the fake news that the Secondary Exams results of Assam had been released. The Minister clarified that the Board of Secondary Education, Assam (SEBA) and Assam Higher Secondary Education Council (AHSEC) are responsible for declaring the exam results, and they will be declared according to their predetermined schedule.
Additionally, Minister Ranoj Pegu shared screenshots of the fake Twitter account bearing his name and allegedly spreading false news about the announcement of results for the HSLC & HS Examination, 2024. The screenshots revealed that miscreants had attempted to spread the fake news that the results of the Secondary Exams would be declared on Saturday, April 20, 2024.
Minister Ranoj Pegu also clarified that the claims were entirely false and once again exposed how easily such false information can spread on social media. This underscores the need for readers to remain vigilant and verify information from credible sources.
SEBA and AHSEC are tasked with conducting the Class 10 and Class 12 exams, respectively. The Class 10 matric exams concluded on March 4, and the Class 12 higher secondary exams concluded on March 13. In 2023, the Assam board Class 10 results were declared on May 22, and Class 12 HS results on June 16. The results will be made available on the official websites of the board — sebaonline.org, resultsassam.nic.in, and ahsec.assam.gov.in.
Last year, the pass percentage for Class 10 was 72.69 percent. The pass percentage for the Class 12 Arts stream was 70.12 percent, 79.57 percent for the Commerce stream, and 84.96 percent in the Science stream.
The Assam Board of Secondary Education is expected to release the Assam Board 10th Result 2024 during the first week of May 2024. However, no official announcement has been issued by the Assam Board yet.
Also Read: 911 Outage In US: China Cyberattack Hacking Theories Explored
NASA Providing Internship Opportunities: Check Last Date To Apply, Eligibility Criteria, and Other Details Published
4 weeks ago on
April 9, 2024 The legendary National Aeronautics and Space Administration, NASA, is currently looking to appoint interns!
The Fall 2024 Internship Session is currently being opened by the leading space agency and inviting applications from interested individuals, reported NASA .
Interested candidates and students can apply for the internship provided by NASA on intern.nasa.gov ., their official website.
NASA’s Office of STEM Engagement on an annual basis accepts enrollment of over 2,000 students via this opportunity.
Under NASA’s pathways programme, recent graduates and students are allowed to apply for “paid internships that are direct pipelines to full-time employment at NASA”.
NASA provides internship opportunities for non-STEM students as well.
The leading space agency announced,
“A common misconception is that NASA only offers engineering internships. Please know that we have opportunities for students who are not majoring in engineering. NASA needs employees with a variety of knowledge and skills. At NASA, our engineers, mathematicians, scientists, accountants, writers, IT specialists, project managers, program analysts, and many other professionals work together to break barriers to achieve the seemingly impossible.”
NASA further added,
“Non-engineering interns may support a variety of business and program management work, including procurement, budgeting, accounting, information technology, and security.”
Eligibility Criteria of NASA Internship The eligibility criteria for the internship is also an important factor to be taken care of. To apply for the internship, candidates must hold US citizenship and have a minimum GPA from 3.0 to 4.0 on a scale of five.
Candidates of 16 years or older can apply for the internship. The last date to fill up the application form for NASA’s internship programme is April 12, 2024.
How To Apply For NASA Internship 1. Visit interns.nasa.gov ., the official website of NASA.
2. Check the website and scroll down on the homepage where “Apply Here” is written. (Direct Link provided)
3. Fill in the application form and upload all the required documents.
4. Recheck the application form and submit it.
5. Save a copy of the application form for future use.
Also Read: NASA Chooses Three Companies to Develop Vehicle for Moon Surface Exploration
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
(adsbygoogle = window.adsbygoogle || []).push({});
if (window.innerWidth < 768) { jQuery(document).find('.ays-pb-modal_2').css({'top': '0', 'right': '0', 'bottom': '0', 'left': '0'}); } else { jQuery(document).find('.ays-pb-modal_2').css({'top': '0', 'right': '0', 'bottom': '0', 'left': '0'}); }
(function( $ ) {
'use strict';
$(document).ready(function(){
let pbViewsFlag_2 = true;
if ('image_type_img_theme' == 'notification') {
$(document).find('.ays-pb-modals').prependTo($(document.body));
} else {
$(document).find('.ays-pb-modals:not(.ays-pb-modals.ays-pb-notification-modal)').appendTo($(document.body));
}
let isMobile = false;
let closePopupOverlay = 1;
let isPageScrollDisabled = 0;
let checkAnimSpeed = 1;
let ays_pb_animation_close_speed = $(document).find('#ays_pb_animation_close_speed_2').val();
let ays_pb_effectIn_2 = $(document).find('#ays_pb_modal_animate_in_2').val();
let ays_pb_effectOut_2 = $(document).find('#ays_pb_modal_animate_out_2').val();
if (window.innerWidth < 768) {
isMobile = true;
closePopupOverlay = 1;
isPageScrollDisabled = 0;
checkAnimSpeed = 1;
ays_pb_animation_close_speed = $(document).find('#ays_pb_animation_close_speed_mobile_2').val();
ays_pb_effectIn_2 = $(document).find('#ays_pb_modal_animate_in_mobile_2').val();
ays_pb_effectOut_2 = $(document).find('#ays_pb_modal_animate_out_mobile_2').val();
}
let ays_pb_delayOpen_2 = parseInt($(document).find('.ays_pb_delay_2').val());
let ays_pb_scrollTop_2 = parseInt($(document).find('.ays_pb_scroll_2').val());
if (isMobile) {
if (0) {
ays_pb_scrollTop_2= parseInt($(document).find('.ays_pb_scroll_mobile_2').val());
}if (0) {
ays_pb_delayOpen_2 = parseInt($(document).find('.ays_pb_delay_mobile_2').val());
}
}
let time_pb_2 = $(document).find('.ays_pb_timer_2 span').data('seconds'),
ays_pb_animation_close_seconds = (ays_pb_animation_close_speed / 1000);
if( ays_pb_delayOpen_2 == 0 && ays_pb_scrollTop_2 == 0){
$(document).find('.av_pop_modals_2').css('display','block');
}if (window.innerWidth < 768) {
var mobileTimer = +$(document).find('.ays_pb_timer_2 span').attr('data-ays-mobile-seconds');
$(document).find('.ays_pb_timer_2 span').html(mobileTimer);
time_pb_2 = mobileTimer;
}ays_pb_animation_close_speed = parseFloat(ays_pb_animation_close_speed) - 50;$(document).find('.ays_music_sound').css({'display':'none'});
if(time_pb_2 !== undefined){
if(time_pb_2 !== 0){
$(document).find('#ays-pb-modal-checkbox_2').trigger('click');
if(ays_pb_scrollTop_2 == 0){
var ays_pb_flag = true;
$(document).find('.ays-pb-modal_2').css({
'animation-duration': ays_pb_animation_close_seconds + 's'
});
let timer_pb_2 = setInterval(function(){
let newTime_pb_2 = time_pb_2--;
$(document).find('.ays_pb_timer_2 span').text(newTime_pb_2);
if(newTime_pb_2 <= 0){
$(document).find('.ays-pb-modal-close_2').trigger('click');
$(document).find('.ays-pb-modal_2').attr('class', 'ays-pb-modal ays-pb-modal-image-type-img ays-pb-modal_2 ays-pb-border-mobile_2 '+ays_pb_effectOut_2);
if(ays_pb_effectOut_2 != 'none'){
setTimeout(function(){
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
}, ays_pb_animation_close_speed);
}else{
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
}
clearInterval(timer_pb_2);
}
$(document).find('.ays-pb-modal-close_2').one('click', function(){
if (pbViewsFlag_2) {
var pb_id = 2;$.ajax({
url: pbLocalizeObj.ajax,
method: 'POST',
dataType: 'text',
data: {
id: pb_id,
action: 'ays_increment_pb_views',
},
});pbViewsFlag_2 = false;
}
$(document).find('.av_pop_modals_2').css('pointer-events', 'none');
$(document).find('.ays-pb-modal_2').attr('class', 'ays-pb-modal ays-pb-modal-image-type-img ays-pb-modal_2 ays-pb-border-mobile_2 '+ays_pb_effectOut_2);
$(this).parents('.ays-pb-modals').find('iframe').each(function(){
var key = /https:\/\/www.youtube.com/;
var src = $(this).attr('src');
$(this).attr('src', $(this).attr('src'));
});
$(this).parents('.ays-pb-modals').find('video.wp-video-shortcode').each(function(){
if(typeof $(this).get(0) != 'undefined'){
if ( ! $(this).get(0).paused ) {
$(this).get(0).pause();
}
}
});
$(this).parents('.ays-pb-modals').find('audio.wp-audio-shortcode').each(function(){
if(typeof $(this).get(0) != 'undefined'){
if ( ! $(this).get(0).paused ) {
$(this).get(0).pause();
}
}
});
var close_sound_src = $(document).find('#ays_pb_close_sound_2').attr('src');
if(checkAnimSpeed && typeof close_sound_src !== 'undefined' && 'off' === 'on'){
if(checkAnimSpeed !== 0){
var playPromise = $(document).find('#ays_pb_close_sound_2').get(0).play();
if (playPromise !== undefined) {
playPromise.then(function() {
audio.pause();
}).catch(function(error) {
});
}
}
}
if(ays_pb_effectOut_2 != 'none'){
setTimeout(function(){
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.av_pop_modals_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
if($('#ays_pb_close_sound_2').get(0) != undefined){
if(!$('#ays_pb_close_sound_2').get(0).paused){
$(document).find('.ays-pb-modal_2').css('display', 'none');
var audio = $('#ays_pb_close_sound_2').get(0);
audio.pause();
audio.currentTime = 0;
}
}
}, ays_pb_animation_close_speed);
}else{
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.av_pop_modals_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
if($('#ays_pb_close_sound_2').get(0) != undefined){
if(!$('#ays_pb_close_sound_2').get(0).paused){
$(document).find('.ays-pb-modal_2').css('display', 'none');
var audio = $('#ays_pb_close_sound_2').get(0);
audio.pause();
audio.currentTime = 0;
}
}
}
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0', 'display': 'none'});
clearInterval(timer_pb_2);
});
$(document).on('keydown', function(event) {
if('1' && ays_pb_flag){
var escClosingPopups = $(document).find('.ays-pb-close-popup-with-esc:visible');
if (event.keyCode == 27) {
var topmostPopup = escClosingPopups.last();
topmostPopup.find('.ays-pb-modal-close_2').trigger('click');
}
} else {
ays_pb_flag = true;
}
ays_pb_flag = false;
});
},1000);
if(closePopupOverlay && 'On' == 'On'){
$(document).find('.av_pop_modals_2').on('click', function(e) {
var pb_parent = $(this);
var pb_div = $(this).find('.ays-pb-modal_2');
if (!pb_div.is(e.target) && pb_div.has(e.target).length === 0){
$(document).find('.ays-pb-modal-close_2').click();
}
});
}
}
} else {
$(document).find('.ays_pb_timer_2').css('display','none');
$(document).find('.ays-pb-modal_2').css({
'animation-duration': ays_pb_animation_close_seconds + 's'
});
$(document).find('.ays-pb-modal-close_2').one('click', function(){
if (pbViewsFlag_2) {
var pb_id = 2;$.ajax({
url: pbLocalizeObj.ajax,
method: 'POST',
dataType: 'text',
data: {
id: pb_id,
action: 'ays_increment_pb_views',
},
});pbViewsFlag_2 = false;
}
$(document).find('.av_pop_modals_2').css('pointer-events', 'none');
$(document).find('.ays-pb-modal_2').attr('class', 'ays-pb-modal ays-pb-modal-image-type-img ays-pb-modal_2 ays-pb-border-mobile_2 '+ays_pb_effectOut_2);
$(this).parents('.ays-pb-modals').find('iframe').each(function(){
var key = /https:\/\/www.youtube.com/;
var src = $(this).attr('src');
$(this).attr('src', $(this).attr('src'));
});
$(this).parents('.ays-pb-modals').find('video.wp-video-shortcode').each(function(){
if(typeof $(this).get(0) != 'undefined'){
if ( ! $(this).get(0).paused ) {
$(this).get(0).pause();
}
}
});
$(this).parents('.ays-pb-modals').find('audio.wp-audio-shortcode').each(function(){
if(typeof $(this).get(0) != 'undefined'){
if ( ! $(this).get(0).paused ) {
$(this).get(0).pause();
}
}
});
if(ays_pb_effectOut_2 != 'none'){
setTimeout(function(){
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.av_pop_modals_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
if($('#ays_pb_close_sound_2').get(0) != undefined){
if(!$('#ays_pb_close_sound_2').get(0).paused){
$(document).find('.ays-pb-modal_2').css('display', 'none');
var audio = $('#ays_pb_close_sound_2').get(0);
audio.pause();
audio.currentTime = 0;
}
}
}, ays_pb_animation_close_speed);
}else{
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.av_pop_modals_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
if($('#ays_pb_close_sound_2').get(0) != undefined){
if(!$('#ays_pb_close_sound_2').get(0).paused){
$(document).find('.ays-pb-modal_2').css('display', 'none');
var audio = $('#ays_pb_close_sound_2').get(0);
audio.pause();
audio.currentTime = 0;
}
}
}
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0', 'display': 'none'});
});
}
}
let count = 0;
if( ays_pb_scrollTop_2 !== 0 ){
$(window).scroll(function() {
if(($(this).scrollTop() >= ays_pb_scrollTop_2) && (count === 0)) {
count++;
if( ays_pb_delayOpen_2 !== 0 ){
$(document).find('.ays-pb-modal_2').css('animation-delay', ays_pb_delayOpen_2/1000);
setTimeout(function(){
$(document).find('.av_pop_modals_2').css('display','block');
$(document).find('.ays-pb-modal_2').addClass(ays_pb_effectIn_2);
$(document).find('.ays-pb-modal_2').css('display', 'block');
if (window.innerWidth < 768 && $(document).find('#ays-pb-screen-shade_2').attr('data-mobile-overlay') == 'true') {
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.5'});
}
else{
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.500000'});
}$(document).find('.ays-pb-modal-check_2').prop('checked', true);
}, ays_pb_delayOpen_2);
}else{
$(document).find('.av_pop_modals_2').css('display','block');
$(document).find('.ays-pb-modal_2').addClass(ays_pb_effectIn_2);
$(document).find('.ays-pb-modal_2').css('display', 'block');
if (window.innerWidth < 768 && $(document).find('#ays-pb-screen-shade_2').attr('data-mobile-overlay') == 'true') {
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.5'});
}
else{
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.500000'});
}$(document).find('.ays-pb-modal-check_2').prop('checked', true);
}
if('false' == 'true' && window.innerWidth < 768){
if(0 != 0 && 'off' != 'on'){
let close_button_delay_for_mobile = 0;
if (ays_pb_delayOpen_2 != 0) {
close_button_delay_for_mobile += Math.floor(ays_pb_delayOpen_2);
}
$(document).find('.ays-pb-modal-close_2').css({'display': 'none'});
setTimeout(function(){
$(document).find('.ays-pb-modal-close_2').css({'display': 'block'});
}, close_button_delay_for_mobile );
}
}
else {
if(0 != 0 && 'off' != 'on'){
let close_button_delay = 0;
if (ays_pb_delayOpen_2 != 0) {
close_button_delay += Math.floor(ays_pb_delayOpen_2);
}
$(document).find('.ays-pb-modal-close_2').css({'display': 'none'});
setTimeout(function(){
$(document).find('.ays-pb-modal-close_2').css({'display': 'block'});
}, close_button_delay );
}
}
if(5 != 0){
$(document).find('.ays-pb-modal_2').css({
'animation-duration': ays_pb_animation_close_seconds + 's'
});
let timer_pb_2 = setInterval(function(){
let newTime_pb_2 = time_pb_2--;
$(document).find('.ays_pb_timer_2 span').text(newTime_pb_2);
if(newTime_pb_2 <= 0){
$(document).find('.ays-pb-modal-close_2').trigger('click');
$(document).find('.ays-pb-modal_2').attr('class', 'ays-pb-modal ays-pb-modal-image-type-img ays-pb-modal_2 '+ays_pb_effectOut_2);
if(ays_pb_effectOut_2 != 'none'){
setTimeout(function(){
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
}, ays_pb_animation_close_speed);
}else{
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
}
clearInterval(timer_pb_2);
}
$(document).find('.ays-pb-modal-close_2').one('click', function(){
if (pbViewsFlag_2) {
var pb_id = 2;$.ajax({
url: pbLocalizeObj.ajax,
method: 'POST',
dataType: 'text',
data: {
id: pb_id,
action: 'ays_increment_pb_views',
},
});pbViewsFlag_2 = false;
}
$(document).find('.av_pop_modals_2').css('pointer-events', 'none');
$(document).find('.ays-pb-modal_2').attr('class', 'ays-pb-modal ays-pb-modal-image-type-img ays-pb-modal_2 ays-pb-border-mobile_2 '+ays_pb_effectOut_2);
$(this).parents('.ays-pb-modals').find('iframe').each(function(){
var key = /https:\/\/www.youtube.com/;
var src = $(this).attr('src');
$(this).attr('src', $(this).attr('src'));
});
$(this).parents('.ays-pb-modals').find('video.wp-video-shortcode').each(function(){
if(typeof $(this).get(0) != 'undefined'){
if ( ! $(this).get(0).paused ) {
$(this).get(0).pause();
}
}
});
$(this).parents('.ays-pb-modals').find('audio.wp-audio-shortcode').each(function(){
if(typeof $(this).get(0) != 'undefined'){
if ( ! $(this).get(0).paused ) {
$(this).get(0).pause();
}
}
});
if(ays_pb_effectOut_2 != 'none'){
setTimeout(function(){
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.av_pop_modals_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
if($('#ays_pb_close_sound_2').get(0) != undefined){
if(!$('#ays_pb_close_sound_2').get(0).paused){
$(document).find('.ays-pb-modal_2').css('display', 'none');
var audio = $('#ays_pb_close_sound_2').get(0);
audio.pause();
audio.currentTime = 0;
}
}
}, ays_pb_animation_close_speed);
}else{
$(document).find('.ays-pb-modal_2').css('display', 'none');
$(document).find('.av_pop_modals_2').css('display', 'none');
$(document).find('.ays-pb-modal_2').attr('data-ays-flag','true');
if($('#ays_pb_close_sound_2').get(0) != undefined){
if(!$('#ays_pb_close_sound_2').get(0).paused){
$(document).find('.ays-pb-modal_2').css('display', 'none');
var audio = $('#ays_pb_close_sound_2').get(0);
audio.pause();
audio.currentTime = 0;
}
}
}
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0', 'display': 'none'});
clearInterval(timer_pb_2);
});
var ays_pb_flag = true;
$(document).on('keydown', function(event) {
if('1' && ays_pb_flag){
var escClosingPopups = $(document).find('.ays-pb-close-popup-with-esc:visible');
if (event.keyCode == 27) {
var topmostPopup = escClosingPopups.last();
topmostPopup.find('.ays-pb-modal-close_2').trigger('click');
ays_pb_flag = false;
}
} else {
ays_pb_flag = true;
}
});
},1000);
}
}
});
}else{
if( ays_pb_delayOpen_2 !== 0 ){
$(document).find('.ays-pb-modal_2').css('animation-delay', ays_pb_delayOpen_2/1000);
setTimeout(function(){
$(document).find('.av_pop_modals_2').css('display','block');
$(document).find('.ays-pb-modal_2').addClass(ays_pb_effectIn_2);
$(document).find('.ays-pb-modal_2').css('display', 'block');
if (window.innerWidth < 768 && $(document).find('#ays-pb-screen-shade_2').attr('data-mobile-overlay') == 'true') {
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.5'});
}
else{
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.500000'});
}
$(document).find('.ays-pb-modal-check_2').attr('checked', 'checked');if(isPageScrollDisabled){
$(document).find('body').addClass('pb_disable_scroll_2');
$(document).find('html').removeClass('pb_enable_scroll');
}}, ays_pb_delayOpen_2);
} else {
if($(document).find('.ays_pb_abt_2').val() != 'clickSelector'){
$(document).find('.av_pop_modals_2').css('display','block');
$(document).find('.ays-pb-modal_2').addClass(ays_pb_effectIn_2);
$(document).find('.ays-pb-modal_2').css('display', 'block');
if (window.innerWidth < 768 && $(document).find('#ays-pb-screen-shade_2').attr('data-mobile-overlay') == 'true') {
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.5'});
}
else{
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0.500000'});
}
$(document).find('.ays-pb-modal-check_2').attr('checked', 'checked');if(isPageScrollDisabled){
$(document).find('body').addClass('pb_disable_scroll_2');
$(document).find('html').addClass('pb_disable_scroll_2');
}
}
}
}
if ('On' != 'On'){
$(document).find('#ays-pb-screen-shade_2').css({'opacity': '0', 'display': 'none !important', 'pointer-events': 'none', 'background': 'none'});
$(document).find('.ays-pb-modal_2').css('pointer-events', 'auto');
$(document).find('.av_pop_modals_2').css('pointer-events','none');
};
if($(document).find('.ays-pb-modals video').hasClass('wp-video-shortcode')){
var videoWidth = $(document).find('.ays-pb-modals video.wp-video-shortcode').attr('width');
var videoHeight = $(document).find('.ays-pb-modals video.wp-video-shortcode').attr('height');
setTimeout(function(){
$(document).find('.ays-pb-modals .wp-video').removeAttr('style');
$(document).find('.ays-pb-modals .mejs-container').removeAttr('style');
$(document).find('.ays-pb-modals video.wp-video-shortcode').removeAttr('style');$(document).find('.ays-pb-modals .wp-video').css({'width': '100%'});
$(document).find('.ays-pb-modals .mejs-container').css({'width': '100%','height': videoHeight + 'px'});
$(document).find('.ays-pb-modals video.wp-video-shortcode').css({'width': '100%','height': videoHeight + 'px'});
},1000);
}
if($(document).find('.ays-pb-modals iframe').attr('style') != ''){
setTimeout(function(){
$(document).find('.ays-pb-modals iframe').removeAttr('style');
},500);
}
// if(5 == 0){
if(closePopupOverlay && 'On' == 'On'){
$(document).find('.av_pop_modals_2').on('click', function(e) {
var pb_parent = $(this);
var pb_div = $(this).find('.ays-pb-modal_2');
if (!pb_div.is(e.target) && pb_div.has(e.target).length === 0){
$(document).find('.ays-pb-modal-close_2').click();
}
});
}
var ays_pb_flag = true;
$(document).on('keydown', function(event) {
if('1' && ays_pb_flag){
var escClosingPopups = $(document).find('.ays-pb-close-popup-with-esc:visible');
if (event.keyCode == 27) {
var topmostPopup = escClosingPopups.last();
topmostPopup.find('.ays-pb-modal-close_2').trigger('click');
ays_pb_flag = false;
}
} else {
ays_pb_flag = true;
}
});
// }
if('off' == 'on') {
var video = $(document).find('video.wp-video-shortcode');
for (let i = 0; i < video.length; i++) {
video[i].addEventListener('ended', function() {
if ($(this).next().val() === 'on') {
$(this).parents('.ays_video_window').find('.close-image-btn').trigger('click');
}
});
}
}
jQuery(document).on('click', '.ays-pb-modal-close_2', function() {
$(document).find('body').removeClass('pb_disable_scroll_2');
$(document).find('html').removeClass('pb_disable_scroll_2');
});});
})( jQuery );
if(typeof aysPopupOptions === "undefined"){
var aysPopupOptions = [];
}
aysPopupOptions["2"] = "eyJwb3B1cGJveCI6eyJpZCI6IjIiLCJ0aXRsZSI6IkFkIiwicG9wdXBfbmFtZSI6IiIsImRlc2NyaXB0aW9uIjoiRGVtbyBEZXNjcmlwdGlvbiIsImNhdGVnb3J5X2lkIjoiMSIsImF1dG9jbG9zZSI6IjUiLCJjb29raWUiOiIxNDQwIiwid2lkdGgiOjQwMCwiaGVpZ2h0Ijo1MDAsImJnY29sb3IiOiIjZmZmZmZmIiwidGV4dGNvbG9yIjoiIzAwMDAwMCIsImJvcmRlcnNpemUiOiIxIiwiYm9yZGVyY29sb3IiOiIjZmZmZmZmIiwiYm9yZGVyX3JhZGl1cyI6IjQiLCJzaG9ydGNvZGUiOiIiLCJ1c2Vyc19yb2xlIjoiW10iLCJjdXN0b21fY2xhc3MiOiIiLCJjdXN0b21fY3NzIjoiIiwiY3VzdG9tX2h0bWwiOiJIZXJlIGNhbiBiZSB5b3VyIGN1c3RvbSBIVE1MIG9yIFNob3J0Y29kZSIsIm9ub2Zmc3dpdGNoIjoiT24iLCJzaG93X29ubHlfZm9yX2F1dGhvciI6Im9mZiIsInNob3dfYWxsIjoiYWxsIiwiZGVsYXkiOiIzIiwic2Nyb2xsX3RvcCI6IjAiLCJhbmltYXRlX2luIjoiZmFkZUluIiwiYW5pbWF0ZV9vdXQiOiJmYWRlT3V0IiwiYWN0aW9uX2J1dHRvbiI6IiIsInZpZXdfcGxhY2UiOiIiLCJhY3Rpb25fYnV0dG9uX3R5cGUiOiJwYWdlTG9hZGVkIiwibW9kYWxfY29udGVudCI6ImltYWdlX3R5cGUiLCJ2aWV3X3R5cGUiOiJpbWFnZV90eXBlX2ltZ190aGVtZSIsIm9ub2Zmb3ZlcmxheSI6Ik9uIiwib3ZlcmxheV9vcGFjaXR5IjoiMC41MDAwMDAiLCJzaG93X3BvcHVwX3RpdGxlIjoiT2ZmIiwic2hvd19wb3B1cF9kZXNjIjoiT2ZmIiwiY2xvc2VfYnV0dG9uIjoib2ZmIiwiaGVhZGVyX2JnY29sb3IiOiIjZmZmZmZmIiwiYmdfaW1hZ2UiOiIiLCJsb2dfdXNlciI6Ik9uIiwiZ3Vlc3QiOiJPbiIsImFjdGl2ZV9kYXRlX2NoZWNrIjoib2ZmIiwiYWN0aXZlSW50ZXJ2YWwiOiIyMDI0LTA0LTE5IDE2OjA0OjE3IiwiZGVhY3RpdmVJbnRlcnZhbCI6IjIwMjQtMDQtMTkgMTY6MDQ6MTciLCJwYl9wb3NpdGlvbiI6ImNlbnRlci1jZW50ZXIiLCJwYl9tYXJnaW4iOiIwIiwidmlld3MiOiI3NjMxMyIsImNvbnZlcnNpb25zIjoiMCIsIm9wdGlvbnMiOiJ7XCJlbmFibGVfYmFja2dyb3VuZF9ncmFkaWVudFwiOlwib2ZmXCIsXCJiYWNrZ3JvdW5kX2dyYWRpZW50X2NvbG9yXzFcIjpcIiMwMDBcIixcImJhY2tncm91bmRfZ3JhZGllbnRfY29sb3JfMlwiOlwiI2ZmZlwiLFwicGJfZ3JhZGllbnRfZGlyZWN0aW9uXCI6XCJ2ZXJ0aWNhbFwiLFwiZW5hYmxlX2JhY2tncm91bmRfZ3JhZGllbnRfbW9iaWxlXCI6XCJvZmZcIixcImJhY2tncm91bmRfZ3JhZGllbnRfY29sb3JfMV9tb2JpbGVcIjpcIiMwMDBcIixcImJhY2tncm91bmRfZ3JhZGllbnRfY29sb3JfMl9tb2JpbGVcIjpcIiNmZmZcIixcInBiX2dyYWRpZW50X2RpcmVjdGlvbl9tb2JpbGVcIjpcInZlcnRpY2FsXCIsXCJleGNlcHRfcG9zdF90eXBlc1wiOltdLFwiZXhjZXB0X3Bvc3RzXCI6W10sXCJhbGxfcG9zdHNcIjpcIlwiLFwiY2xvc2VfYnV0dG9uX2RlbGF5XCI6MCxcImNsb3NlX2J1dHRvbl9kZWxheV9mb3JfbW9iaWxlXCI6MCxcImVuYWJsZV9jbG9zZV9idXR0b25fZGVsYXlfZm9yX21vYmlsZVwiOlwib2ZmXCIsXCJlbmFibGVfcGJfc291bmRcIjpcIm9mZlwiLFwib3ZlcmxheV9jb2xvclwiOlwiIzAwMFwiLFwiZW5hYmxlX292ZXJsYXlfY29sb3JfbW9iaWxlXCI6XCJvZmZcIixcIm92ZXJsYXlfY29sb3JfbW9iaWxlXCI6XCIjMDAwXCIsXCJhbmltYXRpb25fc3BlZWRcIjoxLFwiZW5hYmxlX2FuaW1hdGlvbl9zcGVlZF9tb2JpbGVcIjpcIm9mZlwiLFwiYW5pbWF0aW9uX3NwZWVkX21vYmlsZVwiOjEsXCJjbG9zZV9hbmltYXRpb25fc3BlZWRcIjoxLFwiZW5hYmxlX2Nsb3NlX2FuaW1hdGlvbl9zcGVlZF9tb2JpbGVcIjpcIm9mZlwiLFwiY2xvc2VfYW5pbWF0aW9uX3NwZWVkX21vYmlsZVwiOjEsXCJwYl9tb2JpbGVcIjpcIm9mZlwiLFwiY2xvc2VfYnV0dG9uX3RleHRcIjpcIlxcdTI3MTVcIixcImVuYWJsZV9jbG9zZV9idXR0b25fdGV4dF9tb2JpbGVcIjpcIm9uXCIsXCJjbG9zZV9idXR0b25fdGV4dF9tb2JpbGVcIjpcIlxcdTI3MTVcIixcImNsb3NlX2J1dHRvbl9ob3Zlcl90ZXh0XCI6XCJcIixcIm1vYmlsZV93aWR0aFwiOlwiXCIsXCJtb2JpbGVfbWF4X3dpZHRoXCI6XCJcIixcIm1vYmlsZV9oZWlnaHRcIjpcIlwiLFwiY2xvc2VfYnV0dG9uX3Bvc2l0aW9uXCI6XCJyaWdodC10b3BcIixcImVuYWJsZV9jbG9zZV9idXR0b25fcG9zaXRpb25fbW9iaWxlXCI6XCJvZmZcIixcImNsb3NlX2J1dHRvbl9wb3NpdGlvbl9tb2JpbGVcIjpcInJpZ2h0LXRvcFwiLFwic2hvd19vbmx5X29uY2VcIjpcIm9mZlwiLFwic2hvd19vbl9ob21lX3BhZ2VcIjpcIm9mZlwiLFwiY2xvc2VfcG9wdXBfZXNjXCI6XCJvblwiLFwicG9wdXBfd2lkdGhfYnlfcGVyY2VudGFnZV9weFwiOlwicGl4ZWxzXCIsXCJwb3B1cF9jb250ZW50X3BhZGRpbmdcIjowLFwicG9wdXBfcGFkZGluZ19ieV9wZXJjZW50YWdlX3B4XCI6XCJwaXhlbHNcIixcInBiX2ZvbnRfZmFtaWx5XCI6XCJpbmhlcml0XCIsXCJjbG9zZV9wb3B1cF9vdmVybGF5XCI6XCJvblwiLFwiY2xvc2VfcG9wdXBfb3ZlcmxheV9tb2JpbGVcIjpcIm9uXCIsXCJlbmFibGVfcGJfZnVsbHNjcmVlblwiOlwib2ZmXCIsXCJlbmFibGVfaGlkZV90aW1lclwiOlwib2ZmXCIsXCJlbmFibGVfaGlkZV90aW1lcl9tb2JpbGVcIjpcIm9mZlwiLFwiZW5hYmxlX2F1dG9jbG9zZV9vbl9jb21wbGV0aW9uXCI6XCJvZmZcIixcImVuYWJsZV9zb2NpYWxfbGlua3NcIjpcIm9mZlwiLFwic29jaWFsX2xpbmtzXCI6e1wibGlua2VkaW5fbGlua1wiOlwiXCIsXCJmYWNlYm9va19saW5rXCI6XCJcIixcInR3aXR0ZXJfbGlua1wiOlwiXCIsXCJ2a29udGFrdGVfbGlua1wiOlwiXCIsXCJ5b3V0dWJlX2xpbmtcIjpcIlwiLFwiaW5zdGFncmFtX2xpbmtcIjpcIlwiLFwiYmVoYW5jZV9saW5rXCI6XCJcIn0sXCJzb2NpYWxfYnV0dG9uc19oZWFkaW5nXCI6XCJcIixcImNsb3NlX2J1dHRvbl9zaXplXCI6MSxcImNsb3NlX2J1dHRvbl9pbWFnZVwiOlwiXCIsXCJib3JkZXJfc3R5bGVcIjpcInNvbGlkXCIsXCJlbmFibGVfYm9yZGVyX3N0eWxlX21vYmlsZVwiOlwib2ZmXCIsXCJib3JkZXJfc3R5bGVfbW9iaWxlXCI6XCJzb2xpZFwiLFwiYXlzX3BiX2hvdmVyX3Nob3dfY2xvc2VfYnRuXCI6XCJvZmZcIixcImRpc2FibGVfc2Nyb2xsXCI6XCJvZmZcIixcImRpc2FibGVfc2Nyb2xsX21vYmlsZVwiOlwib2ZmXCIsXCJlbmFibGVfb3Blbl9kZWxheV9tb2JpbGVcIjpcIm9mZlwiLFwib3Blbl9kZWxheV9tb2JpbGVcIjpcIjBcIixcImVuYWJsZV9zY3JvbGxfdG9wX21vYmlsZVwiOlwib2ZmXCIsXCJzY3JvbGxfdG9wX21vYmlsZVwiOlwiMFwiLFwiZW5hYmxlX3BiX3Bvc2l0aW9uX21vYmlsZVwiOlwib2ZmXCIsXCJwYl9wb3NpdGlvbl9tb2JpbGVcIjpcImNlbnRlci1jZW50ZXJcIixcInBiX2JnX2ltYWdlX3Bvc2l0aW9uXCI6XCJjZW50ZXItY2VudGVyXCIsXCJlbmFibGVfcGJfYmdfaW1hZ2VfcG9zaXRpb25fbW9iaWxlXCI6XCJvZmZcIixcInBiX2JnX2ltYWdlX3Bvc2l0aW9uX21vYmlsZVwiOlwiY2VudGVyLWNlbnRlclwiLFwicGJfYmdfaW1hZ2Vfc2l6aW5nXCI6XCJjb3ZlclwiLFwiZW5hYmxlX3BiX2JnX2ltYWdlX3NpemluZ19tb2JpbGVcIjpcIm9mZlwiLFwicGJfYmdfaW1hZ2Vfc2l6aW5nX21vYmlsZVwiOlwiY292ZXJcIixcInZpZGVvX3RoZW1lX3VybFwiOlwiXCIsXCJpbWFnZV90eXBlX2ltZ19zcmNcIjpcImh0dHBzOlxcXC9cXFwvd3d3LnVuaXF1ZW5ld3NvbmxpbmUuY29tXFxcL3dwLWNvbnRlbnRcXFwvdXBsb2Fkc1xcXC8yMDI0XFxcLzA0XFxcL2Jhbm5lci1zYXRzc3BvcnRzLmpwZ1wiLFwiaW1hZ2VfdHlwZV9pbWdfcmVkaXJlY3RfdXJsXCI6XCJodHRwczpcXFwvXFxcL3d3dy5zYXRzcG9ydC5jb21cXFwveFxcXC8jXFxcLzJcXFwvaG9tZVxcXC9leGNoYW5nZVxcXC9zcG9ydFxcXC9hbGw/c2lnbnVwPXRydWUmdXRtX3NvdXJjZT11bmlxdWVuZXdzb25saW5lJnV0bV9tZWRpdW09dW5pcXVlbmV3c29ubGluZVwiLFwiZmFjZWJvb2tfcGFnZV91cmxcIjpcImh0dHBzOlxcXC9cXFwvd3d3LmZhY2Vib29rLmNvbVxcXC93b3JkcHJlc3NcIixcImhpZGVfZmJfcGFnZV9jb3Zlcl9waG90b1wiOlwib2ZmXCIsXCJub3RpZmljYXRpb25fdHlwZV9jb21wb25lbnRzXCI6W10sXCJub3RpZmljYXRpb25fdHlwZV9jb21wb25lbnRzX29yZGVyXCI6e1wibWFpbl9jb250ZW50XCI6XCJtYWluX2NvbnRlbnRcIixcImJ1dHRvbl8xXCI6XCJidXR0b25fMVwifSxcIm5vdGlmaWNhdGlvbl9tYWluX2NvbnRlbnRcIjpcIldyaXRlIHRoZSBjdXN0b20gbm90aWZpY2F0aW9uIGJhbm5lciB0ZXh0IGhlcmUuXCIsXCJub3RpZmljYXRpb25fYnV0dG9uXzFfdGV4dFwiOlwiQ2xpY2shXCIsXCJub3RpZmljYXRpb25fYnV0dG9uXzFfcmVkaXJlY3RfdXJsXCI6XCJcIixcInBiX21heF9oZWlnaHRcIjpcIlwiLFwicG9wdXBfbWF4X2hlaWdodF9ieV9wZXJjZW50YWdlX3B4XCI6XCJwaXhlbHNcIixcInBiX21heF9oZWlnaHRfbW9iaWxlXCI6XCJcIixcInBvcHVwX21heF9oZWlnaHRfYnlfcGVyY2VudGFnZV9weF9tb2JpbGVcIjpcInBpeGVsc1wiLFwicGJfbWluX2hlaWdodFwiOlwiXCIsXCJwYl9mb250X3NpemVcIjoxMyxcInBiX2ZvbnRfc2l6ZV9mb3JfbW9iaWxlXCI6MTMsXCJwYl90aXRsZV90ZXh0X3NoYWRvd1wiOlwicmdiYSgyNTUsMjU1LDI1NSwwKVwiLFwiZW5hYmxlX3BiX3RpdGxlX3RleHRfc2hhZG93XCI6XCJvZmZcIixcInBiX3RpdGxlX3RleHRfc2hhZG93X3hfb2Zmc2V0XCI6MixcInBiX3RpdGxlX3RleHRfc2hhZG93X3lfb2Zmc2V0XCI6MixcInBiX3RpdGxlX3RleHRfc2hhZG93X3pfb2Zmc2V0XCI6MCxcInBiX3RpdGxlX3RleHRfc2hhZG93X21vYmlsZVwiOlwicmdiYSgyNTUsMjU1LDI1NSwwKVwiLFwiZW5hYmxlX3BiX3RpdGxlX3RleHRfc2hhZG93X21vYmlsZVwiOlwib2ZmXCIsXCJwYl90aXRsZV90ZXh0X3NoYWRvd194X29mZnNldF9tb2JpbGVcIjoyLFwicGJfdGl0bGVfdGV4dF9zaGFkb3dfeV9vZmZzZXRfbW9iaWxlXCI6MixcInBiX3RpdGxlX3RleHRfc2hhZG93X3pfb2Zmc2V0X21vYmlsZVwiOjAsXCJjcmVhdGVfZGF0ZVwiOlwiMjAyNC0wNC0xNyAyMDoyOTo1NlwiLFwiY3JlYXRlX2F1dGhvclwiOjMsXCJhdXRob3JcIjpcIntcXFwiaWRcXFwiOlxcXCIzXFxcIixcXFwibmFtZVxcXCI6XFxcIkRyLiBZb2dlbmRyYSBEZXN3YXJcXFwifVwiLFwiZW5hYmxlX2Rpc21pc3NcIjpcIm9mZlwiLFwiZW5hYmxlX2Rpc21pc3NfdGV4dFwiOlwiRGlzbWlzcyBhZFwiLFwiZW5hYmxlX2Rpc21pc3NfbW9iaWxlXCI6XCJvZmZcIixcImVuYWJsZV9kaXNtaXNzX3RleHRfbW9iaWxlXCI6XCJEaXNtaXNzIGFkXCIsXCJlbmFibGVfYm94X3NoYWRvd1wiOlwib2ZmXCIsXCJlbmFibGVfYm94X3NoYWRvd19tb2JpbGVcIjpcIm9mZlwiLFwiYm94X3NoYWRvd19jb2xvclwiOlwiIzAwMFwiLFwiYm94X3NoYWRvd19jb2xvcl9tb2JpbGVcIjpcIiMwMDBcIixcInBiX2JveF9zaGFkb3dfeF9vZmZzZXRcIjowLFwicGJfYm94X3NoYWRvd194X29mZnNldF9tb2JpbGVcIjowLFwicGJfYm94X3NoYWRvd195X29mZnNldFwiOjAsXCJwYl9ib3hfc2hhZG93X3lfb2Zmc2V0X21vYmlsZVwiOjAsXCJwYl9ib3hfc2hhZG93X3pfb2Zmc2V0XCI6MTUsXCJwYl9ib3hfc2hhZG93X3pfb2Zmc2V0X21vYmlsZVwiOjE1LFwiZGlzYWJsZV9zY3JvbGxfb25fcG9wdXBcIjpcIm9mZlwiLFwiZGlzYWJsZV9zY3JvbGxfb25fcG9wdXBfbW9iaWxlXCI6XCJvZmZcIixcInNob3dfc2Nyb2xsYmFyXCI6XCJvZmZcIixcImhpZGVfb25fcGNcIjpcIm9mZlwiLFwiaGlkZV9vbl90YWJsZXRzXCI6XCJvZmZcIixcInBiX2JnX2ltYWdlX2RpcmVjdGlvbl9vbl9tb2JpbGVcIjpcIm9uXCIsXCJjbG9zZV9idXR0b25fY29sb3JcIjpcIiMwMDAwMDBcIixcImNsb3NlX2J1dHRvbl9ob3Zlcl9jb2xvclwiOlwiIzAwMDAwMFwiLFwiYmx1cmVkX292ZXJsYXlcIjpcIm9mZlwiLFwiYmx1cmVkX292ZXJsYXlfbW9iaWxlXCI6XCJvZmZcIixcInBiX2F1dG9jbG9zZV9tb2JpbGVcIjpcIjBcIixcImVuYWJsZV9hdXRvY2xvc2VfZGVsYXlfdGV4dF9tb2JpbGVcIjpcIm9mZlwiLFwiZW5hYmxlX292ZXJsYXlfdGV4dF9tb2JpbGVcIjpcIm9mZlwiLFwib3ZlcmxheV9tb2JpbGVfb3BhY2l0eVwiOlwiMC41XCIsXCJzaG93X3BvcHVwX3RpdGxlX21vYmlsZVwiOlwiT2ZmXCIsXCJzaG93X3BvcHVwX2Rlc2NfbW9iaWxlXCI6XCJPZmZcIixcImVuYWJsZV9hbmltYXRlX2luX21vYmlsZVwiOlwib2ZmXCIsXCJhbmltYXRlX2luX21vYmlsZVwiOlwiZmFkZUluXCIsXCJlbmFibGVfYW5pbWF0ZV9vdXRfbW9iaWxlXCI6XCJvZmZcIixcImFuaW1hdGVfb3V0X21vYmlsZVwiOlwiZmFkZU91dFwiLFwiZW5hYmxlX2Rpc3BsYXlfY29udGVudF9tb2JpbGVcIjpcIm9mZlwiLFwiZW5hYmxlX2JnY29sb3JfbW9iaWxlXCI6XCJvZmZcIixcImJnY29sb3JfbW9iaWxlXCI6XCIjZmZmZmZmXCIsXCJlbmFibGVfYmdfaW1hZ2VfbW9iaWxlXCI6XCJvZmZcIixcImJnX2ltYWdlX21vYmlsZVwiOlwiXCIsXCJlbmFibGVfYm9yZGVyY29sb3JfbW9iaWxlXCI6XCJvZmZcIixcImJvcmRlcmNvbG9yX21vYmlsZVwiOlwiI2ZmZmZmZlwiLFwiZW5hYmxlX2JvcmRlcnNpemVfbW9iaWxlXCI6XCJvZmZcIixcImJvcmRlcnNpemVfbW9iaWxlXCI6XCIxXCIsXCJlbmFibGVfYm9yZGVyX3JhZGl1c19tb2JpbGVcIjpcIm9mZlwiLFwiYm9yZGVyX3JhZGl1c19tb2JpbGVcIjpcIjRcIn0iLCJzaG93X3BvcHVwX3RpdGxlX21vYmlsZSI6Ik9mZiIsInNob3dfcG9wdXBfZGVzY19tb2JpbGUiOiJPZmYifX0=";
!function(){const e=document.createElement("script");e.async=!0,e.setAttribute("crossorigin","anonymous"),e.src="//pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-9548258067481809";let t=0;document.addEventListener("mousemove",function(){1==++t&&document.getElementsByTagName("HEAD").item(0).appendChild(e)}),window.onscroll=function(n){1==++t&&document.getElementsByTagName("HEAD").item(0).appendChild(e)},setTimeout(function(){0===t&&(t++,document.getElementsByTagName("HEAD").item(0).appendChild(e))},5e3)}();
https://www.uniquenewsonline.com/wp-content/plugins/theia-sticky-sidebar/js/ResizeSensor.js
https://www.uniquenewsonline.com/wp-content/plugins/theia-sticky-sidebar/js/theia-sticky-sidebar.js
https://www.uniquenewsonline.com/wp-content/plugins/theia-sticky-sidebar/js/main.js
https://www.uniquenewsonline.com/wp-content/themes/zox-news/js/mvpcustom.js
jQuery(document).ready(function($) {
var leaderHeight = $("#mvp-leader-wrap").outerHeight();
var navHeight = $("#mvp-main-head-wrap").outerHeight();
var headerHeight = navHeight + leaderHeight;
var previousScroll = 0;
$(window).scroll(function(event){
var scroll = $(this).scrollTop();
if ( typeof leaderHeight !== "undefined" ) {
if ($(window).scrollTop() > headerHeight){
$("#mvp-main-nav-small").addClass("mvp-nav-small-fixed");
$("#mvp-main-body-wrap").css("margin-top", navHeight );
} else {
$("#mvp-main-nav-small").removeClass("mvp-nav-small-fixed");
$("#mvp-main-body-wrap").css("margin-top","0");
}
if ($(window).scrollTop() > headerHeight + 50){
$("#mvp-main-nav-small").addClass("mvp-fixed");
$("#mvp-main-nav-small").addClass("mvp-fixed-shadow");
$(".mvp-fly-top").addClass("mvp-to-top");
if(scroll < previousScroll) {
$("#mvp-main-nav-small").removeClass("mvp-soc-mob-up");
$("#mvp-soc-mob-wrap").removeClass("mvp-soc-mob-up");
$(".mvp-drop-nav-title").removeClass("mvp-nav-small-post");
$(".mvp-nav-menu").show();
} else {
$("#mvp-main-nav-small").addClass("mvp-soc-mob-up");
$("#mvp-soc-mob-wrap").addClass("mvp-soc-mob-up");
$(".mvp-drop-nav-title").addClass("mvp-nav-small-post");
$(".mvp-nav-menu").hide();
}
} else {
$("#mvp-main-nav-small").removeClass("mvp-fixed");
$("#mvp-main-nav-small").removeClass("mvp-fixed-shadow");
$(".mvp-fly-top").removeClass("mvp-to-top");
}
} else {
if ($(window).scrollTop() > navHeight){
$("#mvp-main-nav-small").addClass("mvp-nav-small-fixed");
$("#mvp-main-body-wrap").css("margin-top", navHeight );
} else {
$("#mvp-main-nav-small").removeClass("mvp-nav-small-fixed");
$("#mvp-main-body-wrap").css("margin-top","0");
}
if ($(window).scrollTop() > navHeight + 50){
$("#mvp-main-nav-small").addClass("mvp-fixed");
$("#mvp-main-nav-small").addClass("mvp-fixed-shadow");
$(".mvp-fly-top").addClass("mvp-to-top");
if(scroll < previousScroll) {
$("#mvp-main-nav-small").removeClass("mvp-soc-mob-up");
$("#mvp-soc-mob-wrap").removeClass("mvp-soc-mob-up");
$(".mvp-drop-nav-title").removeClass("mvp-nav-small-post");
$(".mvp-nav-menu").show();
} else {
$("#mvp-main-nav-small").addClass("mvp-soc-mob-up");
$("#mvp-soc-mob-wrap").addClass("mvp-soc-mob-up");
$(".mvp-drop-nav-title").addClass("mvp-nav-small-post");
$(".mvp-nav-menu").hide();
}
} else {
$("#mvp-main-nav-small").removeClass("mvp-fixed");
$("#mvp-main-nav-small").removeClass("mvp-fixed-shadow");
$(".mvp-fly-top").removeClass("mvp-to-top");
}
}
previousScroll = scroll;
});
});jQuery(document).ready(function($) {
// Video Post Scroll
$(window).on("scroll.video", function(event){
var scrollTop = $(window).scrollTop();
var elementOffset = $("#mvp-content-wrap").offset().top;
var distance = (elementOffset - scrollTop);
var aboveHeight = $("#mvp-video-embed-wrap").outerHeight();
if ($(window).scrollTop() > distance + aboveHeight + screen.height){
$("#mvp-video-embed-cont").addClass("mvp-vid-fixed");
$("#mvp-video-embed-wrap").addClass("mvp-vid-height");
$(".mvp-video-close").show();
} else {
$("#mvp-video-embed-cont").removeClass("mvp-vid-fixed");
$("#mvp-video-embed-wrap").removeClass("mvp-vid-height");
$(".mvp-video-close").hide();
}
});$(".mvp-video-close").on("click", function(){
$("#mvp-video-embed-cont").removeClass("mvp-vid-fixed");
$("#mvp-video-embed-wrap").removeClass("mvp-vid-height");
$(".mvp-video-close").hide();
$(window).off("scroll.video");
});});jQuery(document).ready(function($) {
// Mobile Social Buttons More
$(".mvp-soc-mob-right").on("click", function(){
$("#mvp-soc-mob-wrap").toggleClass("mvp-soc-mob-more");
});
});jQuery(document).ready(function($) {
$(".menu-item-has-children a").click(function(event){
event.stopPropagation();});$(".menu-item-has-children").click(function(){
$(this).addClass("toggled");
if($(".menu-item-has-children").hasClass("toggled"))
{
$(this).children("ul").toggle();
$(".mvp-fly-nav-menu").getNiceScroll().resize();
}
$(this).toggleClass("tog-minus");
return false;
});// Main Menu Scroll
$(".mvp-fly-nav-menu").niceScroll({cursorcolor:"#888",cursorwidth: 7,cursorborder: 0,zindex:999999});
});
https://www.uniquenewsonline.com/wp-content/themes/zox-news/js/scripts.js
https://www.uniquenewsonline.com/wp-content/themes/zox-news/js/retina.js
https://www.uniquenewsonline.com/wp-content/themes/zox-news/js/flexslider.js
https://www.uniquenewsonline.com/wp-includes/js/comment-reply.min.js
(function(w,d, s, id) {w.webpushr=w.webpushr||function(){(w.webpushr.q=w.webpushr.q||[]).push(arguments)};var js, fjs = d.getElementsByTagName(s)[0];js = d.createElement(s); js.async=1; js.id = id;js.src = "https://cdn.webpushr.com/app.min.js";
d.body.appendChild(js);}(window,document, 'script', 'webpushr-jssdk'));
webpushr('setup',{'key':'BPjbvHzuEYRqFV4yiEu3fIxgQ_hu6jxsQjNdj6baiXPpbFathx1pQk1KL7M1lXEoliGJckK0dG6UeYUZuTIiCRQ','sw':'https://www.uniquenewsonline.com/wp-content/plugins/webpushr-web-push-notifications/sdk_files/webpushr-sw.js.php'});
window.lazyLoadOptions = {
elements_selector: "iframe[data-lazy-src]",
data_src: "lazy-src",
data_srcset: "lazy-srcset",
data_sizes: "lazy-sizes",
class_loading: "lazyloading",
class_loaded: "lazyloaded",
threshold: 300,
callback_loaded: function(element) {
if ( element.tagName === "IFRAME" && element.dataset.rocketLazyload == "fitvidscompatible" ) {
if (element.classList.contains("lazyloaded") ) {
if (typeof window.jQuery != "undefined") {
if (jQuery.fn.fitVids) {
jQuery(element).parent().fitVids();
}
}
}
}
}};
window.addEventListener('LazyLoad::Initialized', function (e) {
var lazyLoadInstance = e.detail.instance;if (window.MutationObserver) {
var observer = new MutationObserver(function(mutations) {
var image_count = 0;
var iframe_count = 0;
var rocketlazy_count = 0;mutations.forEach(function(mutation) {
for (i = 0; i < mutation.addedNodes.length; i++) {
if (typeof mutation.addedNodes[i].getElementsByTagName !== 'function') {
return;
}if (typeof mutation.addedNodes[i].getElementsByClassName !== 'function') {
return;
}images = mutation.addedNodes[i].getElementsByTagName('img');
is_image = mutation.addedNodes[i].tagName == "IMG";
iframes = mutation.addedNodes[i].getElementsByTagName('iframe');
is_iframe = mutation.addedNodes[i].tagName == "IFRAME";
rocket_lazy = mutation.addedNodes[i].getElementsByClassName('rocket-lazyload');image_count += images.length;
iframe_count += iframes.length;
rocketlazy_count += rocket_lazy.length;if(is_image){
image_count += 1;
}if(is_iframe){
iframe_count += 1;
}
}
} );if(image_count > 0 || iframe_count > 0 || rocketlazy_count > 0){
lazyLoadInstance.update();
}
} );var b = document.getElementsByTagName("body")[0];
var config = { childList: true, subtree: true };observer.observe(b, config);
}
}, false);
https://www.uniquenewsonline.com/wp-content/plugins/rocket-lazy-load/assets/js/16.1/lazyload.min.js




 Viral1 week ago
Viral1 week ago
 Viral4 days ago
Viral4 days ago
 Viral5 days ago
Viral5 days ago
 Viral1 week ago
Viral1 week ago
 Viral4 days ago
Viral4 days ago
 Net Worth5 days ago
Net Worth5 days ago
 Viral4 days ago
Viral4 days ago
 Viral1 week ago
Viral1 week ago









